Il numero PiGreco è uno dei numeri più importanti della matematica. È presente in molte formule di geometria, di algebra ed in moltissime leggi di fisica.
Normalmente viene indicato con la lettera greca perché è un numero la cui scoperta risale agli antichi greci.
Il suo uso più comune è quello del calcolo della circonferenza e dell’area del cerchio.
Preso un cerchio di raggio la sua area si calcola con la formula
$$ A = πr^2$$
mentre la lunghezza della circonferenza si calcola con la formula
$$ C = 2πr$$
Il valore comunemente usato per è 3,14 ma in realtà il ha infinite cifre decimali che non si ripetono. Un numero del genere è detto irrazionale perchè non si può esprimere come rapporto di due numeri interi.
Ci sono molti modi per calcolare un valore approssimato di . Nella pagina dimostrativa viene implementato un metodo basato sul calcolo delle probabilità.
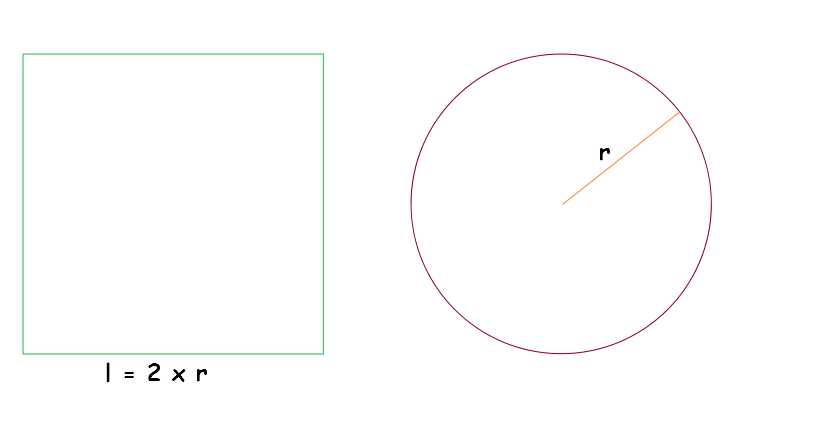
Prendiamo un cerchio di raggio r ed un quadrato di lato l = 2r
L’area del quadrato si calcola con la formula
$$A_q=l^2= (2r)^2 = 4r^2$$
L’area del cerchio sarà invece sicuramente più piccola, quindi invece di 4r2 potremo scrivere
$$A_c= πr^2$$
dove è un valore sconosciuto, sicuramente minore di 4, che vogliamo calcolare.
Ora supponiamo di disegnare le due figure geometriche sulla terra e supponiamo che inizi a piovere. Le gocce di pioggia cadranno sul terreno con una distribuzione uniforme. una certa quantità cadrà nel quadrato ed una quantità diversa (minore) cadrà nel cerchio. Supponiamo di riuscire a contare le gocce cadute nel cerchio e quelle cadute nel quadrato Gc e Gq. Se effettivamente le gocce cadono con una distribuzione uniforme e sono un numero abbastanza elevato possiamo dire che questi due numeri sono quasi proporzionali ai valori delle due aree.
$$\frac {G_c}{G_q}≈ \frac {A_c}{A_q} $$
quindi possiamo scrivere
$$\frac {G_c}{G_q}≈ \frac {πr^2}{4r^2}=\frac{π}{4} $$
da cui si ricava
$$ π ≈4 \frac{G_c}{G_q}$$
Pertanto per avere una stima del valore di basta contare il numero di gocce che cadono nel cerchio, divedere questo numero per il numero di gocce che cadono nel quadrato e moltiplicare il risultato per 4.
Nella pagina dimostrativa invece delle gocce facciamo cadere dei puntini generati casualmente dal computer.
I puntini rossi sono quelli che cadono nel cerchio. I puntini verdi sono quelli che cadono nel quadrato ma al di fuori del cerchio. Quindi i puntini totali che cadono nel quadrato sono la somma dei puntini rossi e dei puntini verdi.